Mientras que la distribución de Poisson describe las llegadas por unidad de tiempo, la distribución exponencial estudia el tiempo entre cada una de estas llegadas. Si las llegadas son de Poisson el tiempo entre estas llegadas es exponencial. Mientras que la distribución de Poisson es discreta la distribución exponencial es continua porque el tiempo entre llegadas no tiene que ser un número entero. Esta distribución se utiliza mucho para describir el tiempo entreeventos. Más específicamente la variable aleatoria que representa al tiempo necesario para servir a la llegada.
Ejemplos típicos de esta situación son el tiempo que un medico dedica a una exploración, el tiempo de servir una medicina en una farmacia, o el tiempo de atender a una urgencia.
El uso de la distribución exponencial supone que los tiempos de servicio son aleatorios, es decir, que un tiempo de servicio determinado no depende de otro servicio realizado anteriormente ni de la posible cola que pueda estar formándose. Otra característica de este tipo de distribución es que no tienen "edad" o en otras palabras, "memoria". Por ejemplo. Supongamos que el tiempo de atención de un paciente en una sala quirúrgica sigue una distribución exponencial. Si el paciente ya lleva 5 horas siendo operado, la probabilidad de que esté una hora más es la misma que si hubiera estado 2 horas, o 10 horas o las que sea. Esto es debido a que la distribución exponencial supone que los tiempos de servicio tienen una gran variabilidad. A lo mejor el próximo paciente operado tarda 1 hora porque su cirugía era mucho más simple que la anterior.
Se dice que la variable aleatoria continua X tiene distribución exponencial con parámetro

Su gráfica es un modelo apropiado a vida útil de objetos.


Par calcular la esperanza matemática y la varianza, se hallara primero el momento de orden r respecto del origen:

CAPITULO II
Distribución exponencial (Práctica)
Ejemplos prácticos sobre la distribución exponencial:
EJEMPLO 1.-El tiempo durante el cual cierta marca de batería trabaja en forma efectiva hasta que falle (tiempo de falla) se distribuye según el modelo exponencial con un tiempo promedio de fallas igual a 360 días.
- a) ¿qué probabilidad hay que el tiempo de falla sea mayor que 400 días?.
- b) Si una de estas baterías ha trabajado ya 400 días, ¿qué probabilidad hay que trabaja más de 200 días más?
- c) Si se están usando 5 de tales baterías calcular la probabilidad de que más de dos de ellas continúen trabajando después de 360 días.
Solución
Sea X=el tiempo que trabaja la batería hasta que falle. El tiempo promedio de falla es de 360 días. Entonces, X ~Exp (ß=1/360) y su función de densidad es:

EJEMPLO 2.-Suponga que la vida de cierto tipo de tubos electrónicos tiene una distribución exponencial con vida media de 500 horas. Si X representa la vida del tubo (tiempo q dura el tubo).
- a) Hallar la probabilidad que se queme antes de las 300 horas.
- b) ¿Cuál es la probabilidad que dure por lo menos 300 horas?
- c) Si un tubo particular ha durado 300 horas. ¿cúal es la probabilidad de que dure otras 400 horas?
Solución

Este, es una propiedad de la distribución exponencial que se conoce como la de no tener memoria.
EJEMPLO 3.-Suponga que el tiempo que necesita un cajero de un banco para atender a un cliente tiene un distribución exponencial con una media de 40 segundos.
- a) Hallar la probabilidad que el tiempo necesario para atender un cliente dado sea mayor que 20 minutos?
- b) ¿Cuál es la probabilidad que el tiempo necesario para atender a un cliente esté comprendido entre 1 y 2 minutos.
Solución

DISTRIBUCCIÓN NORMAL
En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de lasdistribuciones de probabilidad de variable continua que con más frecuencia aparece aproximada en fenómenos reales.[cita requerida]
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.
De hecho, la estadística descriptiva sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:
- caracteres morfológicos de individuos como la estatura;
- caracteres fisiológicos como el efecto de un fármaco;
- caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos;
- caracteres psicológicos como el cociente intelectual;
- nivel de ruido en telecomunicaciones;
- errores cometidos al medir ciertas magnitudes;
- etc.
La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de lasmedias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.1 Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una supuesta "normalidad".
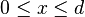

 es el tamaño de población,
es el tamaño de población,  es el tamaño de la muestra extraída,
es el tamaño de la muestra extraída,  es el número de elementos en la población original que pertenecen a la categoría deseada y
es el número de elementos en la población original que pertenecen a la categoría deseada y  es el número de elementos en la muestra que pertenecen a dicha categoría. La notación
es el número de elementos en la muestra que pertenecen a dicha categoría. La notación  hace referencia al
hace referencia al  .
.![E[X]=\frac{nd}{N}](http://upload.wikimedia.org/math/e/d/b/edb7931c237719680795389c71e2ca37.png)
![Var[X]=\bigg(\frac{N-n}{N-1}\bigg)\bigg(\frac{nd}{N}\bigg)\bigg( 1-\frac{d}{N}\bigg).](http://upload.wikimedia.org/math/9/b/2/9b21150dd51ee2e8e3c219b9d6c67cdd.png)


![Var[X]=npq\frac{N-n}{N-1}.](http://upload.wikimedia.org/math/8/4/5/8450776365971ac3ed36f95d91b68b22.png)
 , es el número
, es el número ![\operatorname{E}[X]](http://upload.wikimedia.org/math/8/d/0/8d03ba387a5f20b58a95980a43bdbfa4.png) que formaliza la idea de valor medio de un fenómeno aleatorio.
que formaliza la idea de valor medio de un fenómeno aleatorio.![\begin{align}
\operatorname{E}(X) = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6}
+ 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6}\\[6pt] = \frac{1 + 2 + 3 + 4 + 5 + 6}{6} = 3,5
\end{align}](http://upload.wikimedia.org/math/0/f/a/0fa54d97224666f235b06c03d40c4d8b.png)

 un conjunto de sucesos mutuamente excluyentes y exhaustivos, y tales que la probabilidad de cada uno de ellos es distinta de cero (0). Sea B un suceso cualquiera del que se conocen las probabilidades condicionales
un conjunto de sucesos mutuamente excluyentes y exhaustivos, y tales que la probabilidad de cada uno de ellos es distinta de cero (0). Sea B un suceso cualquiera del que se conocen las probabilidades condicionales  . Entonces, la probabilidad
. Entonces, la probabilidad  viene dada por la expresión:
viene dada por la expresión: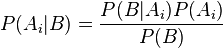
 son las probabilidades a priori.
son las probabilidades a priori. en la hipótesis
en la hipótesis  .
.


 , su función de distribución,
, su función de distribución, 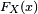 , es
, es
 . Donde en la fórmula anterior:
. Donde en la fórmula anterior: , es la probabilidad definida sobre un
, es la probabilidad definida sobre un  es la medida sobre la
es la medida sobre la 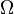 es el
es el  es la variable aleatoria en cuestión, es decir, una función definida sobre el espacio muestral a los números reales.
es la variable aleatoria en cuestión, es decir, una función definida sobre el espacio muestral a los números reales.

 tal que
tal que  , los sucesos
, los sucesos  y
y  son mutuamente excluyentes y su unión es el suceso
son mutuamente excluyentes y su unión es el suceso  , por lo que tenemos entonces que:
, por lo que tenemos entonces que: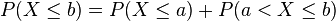


 para todos los valores de la variable aleatoria
para todos los valores de la variable aleatoria