Vídeo:
" https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=6&cad=rja&uact=8&ved=0CFcQtwIwBQ&url=http%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3D78dNjPeLpfE&ei=as4fU86fJ6TN2AW8v4H4Aw&usg=AFQjCNHuoTWi9TCO3oUKEEMsyle286onRQ&sig2=Js4WVntp62E3-B69P9IPgg "
1) Sea A el suceso de sacar un As de una baraja estándar de 52 cartas y B sacar una carta con corazón rojo. Calcular la probabilidad de sacar un As o un corazón rojo o ambos en una sola extracción.
Solución:
A y B son sucesos no mutuamente excluyentes porque puede sacarse el as de corazón rojo.
Las probabilidades son:
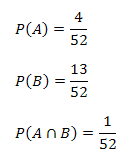
Reemplazando los anteriores valores en la regla general de la adición de probabilidades para eventos no mutuamente excluyentes se obtiene:
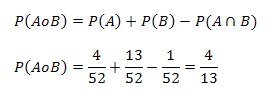
2) En una urna existe 10 bolas numeradas del 1 al 10. ¿Qué probabilidad existe de sacar en una sola extracción una bola enumerada con un número par o con un número primo?
Solución:

O también, realizando un diagrama de Venn-Euler se obtiene:

3) En una clase, 10 alumnos tienen como preferencia solamente la asignatura de Matemática, 15 prefieren solamente Estadística, 20 prefieren Matemática y Estadística y 5 no tienen preferencia por ninguna de estas asignaturas. Calcular la probabilidad que de un alumno de la clase seleccionado al azar tenga preferencia por Matemática o Estadística o ambas asignaturas.
Solución:
Realizando un diagrama de Venn-Euler se obtiene:

Simbología:
S = espacio muestral
A= Matemática
B = Estadística
a = Solamente Matemática
b = Solamente Estadística
c = Matemática y Estadística
d = Ninguna de las dos asignaturas
Datos y cálculos:

Entonces, aplicando la fórmula de la probabilidad teórica se obtiene:

Los cálculos en Excel se muestran en la siguiente figura:

4) En un grupo de 50 personas, 6 tienen como preferencia solamente el color amarrillo, 10 prefieren solamente el color blanco, 6 prefieren el color amarrillo y blanco, 10 prefieren el color blanco y café, 12 prefieren el color amarrillo y café, 4 prefieren los 3 colores y 10 no tienen preferencia por ninguno de los tres colores.
4.1) Elaborar un diagrama de Venn-Euler
4.2) Calcular la probabilidad que de una persona del grupo seleccionada al azar tenga preferencia por lo menos uno de los tres colores.
Solución:

4.2)

Entonces, aplicando la fórmula de la probabilidad teórica se obtiene:

Nota:
Si A, B y C son tres eventos cualesquiera de modo que ocurra A o bien B o bien C o bien los tres a la vez se emplea la regla:

Observando el diagrama de de Venn-Euler se tiene que:

Reemplazando valores en la regla se obtiene:

Los cálculos en se muestran en la siguiente figura:

Leer más: http://www.monografias.com/trabajos88/regla-general-adicion-probabilidades/regla-general-adicion-probabilidades.shtml#ixzz2viKffFcX
No hay comentarios:
Publicar un comentario